6936. Числа, свободные от квадратов
Число называется
свободным от квадратов, если оно не делится ни на один полный квадрат, кроме 1.
Вам необходимо подсчитать их!
Вход. Первая строка содержит количество тестов t. Каждая из следующих t строк содержит одно натуральное число n (n
≤ 1014).
Выход. Вывести t строк, каждая из которых содержит
количество натуральных свободных от квадратов чисел, не больших n.
|
Пример
входа |
Пример
выхода |
|
3 1 1000 100000000000000 |
1 608 60792710185947 |
РЕШЕНИЕ
функция Мебиуса
Анализ алгоритма
Подсчитаем количество натуральных чисел,
не больших n, свободных от квадратов,
используя формулу включения-исключения. Пусть 2 = p1 < p2
< … < pk – множество
всех простых чисел, не больших 
. Тогда по формуле включений-исключений искомое количество
чисел равно
Q(n) = n
– 
+ 
– 
+ …
Пусть n = 30. Имеется три простых числа, не больших 
: p1 =
2, p2 = 3 и p3 = 5. По формуле
Q(30) = 30 – 
– 
– 
+ 
+ 
+ 
– 
= 30 – 7 – 3 – 1 = 19
Если первое слагаемое n рассматривать как n / 12, то можно утверждать, что сумма Q(n) состоит из слагаемых вида 
, где 1 ≤ i
≤ 
(для i > соответствующие суммы
равны нулю). Причем слагаемое имеет знак плюс, если i является произведением четного
количества разных простых чисел, и знак минус, если i является произведением нечетного количества разных простых чисел.
Однако отметим, что в первом случае µ(i) = 1, а во втором µ(i) = -1. Поэтому
значение Q(n) можно переписать через
функцию Мебиуса:
Q(n) =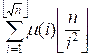 
Учитывая, что
если i свободно от квадратов, то 
= 1. Следовательно
=
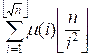
Пример
При n = 30 имеем:
Q(30) = µ(1) 
+ µ(2)
+ µ(3) 
+ µ(4) 
+ µ(5) 
=
= 30 – 7 – 3 + 0
– 1 = 19
Реализация
алгоритма
Объявим
константы и глобальные массивы.
#define MAX 10000010
#define LMAX 700000
int lp[MAX+1] = {0}, primes[LMAX], mu[MAX] = {0};
Линейный Эратосфен. lp[i]
содержит наименьший простой делитель числа i.
void LinearEratosfen(void)
{
int i, j;
for (i = 2; i <= MAX; ++i)
{
if (lp[i] == 0)
{
lp[i] = i;
primes[cnt++] =
i;
}
for (j = 0; j < cnt && primes[j] <=
lp[i] && i * primes[j] <= MAX; j++)
lp[i * primes[j]]
= primes[j];
}
}
Вычисление функции Мебиуса используя массив lp.
void calc_Mobius(void)
{
int i, q;
mu[1] = 1;
for(i = 2; i < MAX; i++)
{
q = i / lp[i];
if (q % lp[i] != 0) mu[i] = -mu[q];
}
}
Основная часть программы. Вычисляем функцию Мебиуса для всех
значений от 1 до MAX.
LinearEratosfen();
calc_Mobius();
Читаем входные данные.
scanf("%d",&tests);
while(tests--)
{
scanf("%lld",&n);
Количество чисел, свободных от квадрратов, вычисляем по
формуле:
Q(n) =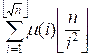
sum = 0; sqn =
sqrt(1.0*n);
for(i = 1; i <= sqn; i++)
sum += (n / (i *
i)) * mu[i];
Выводим ответ.
printf("%lld\n",sum);
}